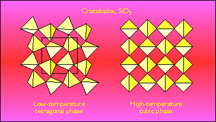

Cristobalite is a form of SiO2 with a relatively simple crystal structure that is closely related to the diamond structure. At around 520 K there is a first-order phase transition between the low-temperature tetragonal phase and the high-temperature cubic phase. Whilst the phase transition appears to be fairly straighforward, it turns out that the basic picture is rather more complicated (and hence controversial!). The essential point is that the crystal structure of the high-temperature cubic phase as determined by X-ray or neutron diffraction does not appear to be chemically reasonable, since it has linear Si-O-Si bonds. In most silicates the angle at the oxygen angle is close to 145 deg. Thus it is more likely that there is considerable disorder in the high-temperature phase that allows these bonds to be bent. This picture is consistent with the large thermal ellipsoids determined in crystal structure refinements, and the fact that the Si-O bond in the average structure is rather shorter than normally found. If in fact the Si-O bonds are canted at an angle of 17 deg from their average orientations, the typical values of the Si-O bond length and Si-O-Si angle are obtained.

The controvery arises over how this disorder can be accomodated within the high-temperature phase. One popular model is that there are small domains of the low-temperature phase, giving the apparent structure of the high-temperature phase as an average over all orientations of these domains. An older model postulates domains of a different symmetry, but the basic ideas are similar. We have suggested instead that the whole picture of the phase transition and structure of the high-temperature phase can be interpreted in terms of our Rigid Unit Mode (RUM) model. Using this model we have found all possible ways to distort the cubic structure that do not require the SiO4 tetrahedra to distort as well. These distortions can be related to phonon modes that lie in planes of wave vectors, and they include the distortions that give rise to the phase transition. The RUM model then suggests that dynamic disorder can arise as a superposition of all the low-energy RUM phonons. This picture is supported by neutron scattering and molecular dynamics simulations.
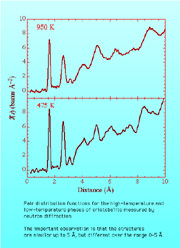
Measurements of the pair distribution function, T(r), for both phases of cristobalite show distinct dfferences over the range 5-10 A, showing that the high-temperature phase does not consist of domains of the low-temperature phase.
Thanks to my collaborators Ian Swainson, now at Chalk River, Dave Keen (ISIS), Alex Hannon (ISIS) and Manoj Gambhir.
Our papers on this subject include (in reverse chronological order):
M T Dove, D A Keen, A C Hannon and I P Swainson, "Direct measurement of the Si-O bond length and orientational disorder in beta-cristobalite". Physics and Chemistry of Minerals (submitted 26/8/96)
Here we use measurements of the total neutron diffraction pattern, Bragg peaks + diffuse scattering, recorded out to 50 1/A, to obtain the pair distribution function T(r). The Si-O and O-O distances are the same in both phases (with a small thermal expansion), consistent with a tilting of the SiO4 tetrahedra by around 17 deg in the cubic phase. The structure over the range 5-10 A in the cubic phase is not like that in the tetragonal phase, suggesting (to me at least) that the cubic structure does not consist of domains of the tetragonal structure. Actually the structure of the cubic phase over this length scale is very similar to that of silica glass.
M Gambhir, V Heine and M T Dove, "A one-parameter model of a rigid-unit structure". Phase Transitions (in press)
This work involved the use of a simple model (actually the same as we use in our Rigid Unit Mode model) to investigate the dynamics and correlations in the cubic phase of cristobalite.
I P Swainson and M T Dove, "Molecular dynamics simulation of alpha- and beta-cristobalite". Journal of Physics: Condensed Matter 7, 1771-1788, 1995.
In this paper we use simulations to show the presence of the dynamic orientational disorder of the SiO4 tetrahedra and give an idea of the time scales involved.
I P Swainson and M T Dove, "On the thermal expansion of beta-cristobalite". Physics and Chemistry of Minerals 22, 61-65, 1995.
Measurements of the thermal expansion of the cubic phase to high temperaures using high-resolution X-ray diffraction are reported. The results are interpreted in terms of the RUM model. The thermal expansion tends to zero at high temperatures.
I P Swainson and M T Dove, "Comment on `First-principles studies on structural properties of beta-cristobalite'". Physical Review Letters 71, 3610, 1993
This adds a small bit to the story.
I P Swainson and M T Dove. "Low-frequency floppy modes in beta-cristobalite". Physical Review Letters 71, 193-196, 1993.
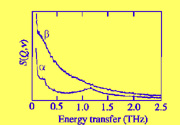
Here we report inelastic neutron scattering data that show the energy scale for the RUMs in the high-temperature phase (0-1 THz). We also use Raman and IR data to argue against the existence of domains with the symmetry of the tetragonal phase at high temperatures.
W W Schmahl, I P Swainson, M T Dove and A Graeme-Barber. "Landau free energy and order parameter behaviour of the alpha/beta phase transition in cristobalite". Zeitschrift fur Kristallographie 201, 125-145, 1992.
This was our first venture into cristobalite. Just to show how unwary we were, this was supposed to be a quick bit of work to get Ian going on his PhD! We use high-resolution neutron diffraction to measure the structure as a function of temperature, and we show that the phase transition can be accurately described within the formalism of Landau theory in spite of the large first-order discontinuity at the phase transition.
Link back to ...